Logarithms


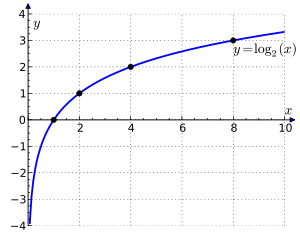
The graph of the logarithm to base 2 crosses the x axis (horizontal axis) at 1 and passes through the points with coordinates (2, 1), (4, 2), and (8, 3). For example, log2(8) = 3, because 2^3 = 8. The graph gets arbitrarily close to the y axis, but does not meet or intersect it.

The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: 1000 = 10^3 = 10 × 10 × 10. More generally, if x = by, then y is the logarithm of x to base b, and is written logb(x), so log10(1000) = 3.
Logarithms were introduced by John Napier in the early 17th century as a means to simplify calculations. They were rapidly adopted by scientists, engineers, and others to perform computations more easily and rapidly, using slide rules and logarithm tables. These devices rely on the fact—important in its own right—that the logarithm of a product is the sum of the logarithms of the factors:

{Log (ab) = Log a + Log b} (1st law of logarithms)


Wikipedia

Googles

Wolfram

Comments

Post a Comment

Popular posts from this blog

Squeeze Theorem - "2 policeman & a drunk"

In calculus, the squeeze theorem (known also as the pinching theorem, the sandwich theorem, the sandwich rule and sometimes the squeeze lemma) is a theorem regarding the limit of a function. The squeeze theorem is a technical result that is very important in proofs in calculus and mathematical analysis. It is typically used to confirm the limit of a function via comparison with two other functions whose limits are known or easily computed. It was first used geometrically by the mathematicians Archimedes and Eudoxus in an effort to compute π, and was formulated in modern terms by Gauss. In Italy, Russia and France, the squeeze theorem is also known as the two carabinieri theorem, two militsioner theorem, two gendarmes theorem, or two policemen and a drunk theorem. The story is that if two policemen are escorting a drunk prisoner between them, and both officers go to a cell, then (regardless of the path taken, and the fact that the prisoner may be wobbling about between the policemen) t...
Read more

Surreal Numbers

Image
In mathematics , the surreal number system is a totally ordered class containing the real numbers as well as infinite and infinitesimal numbers , respectively larger or smaller in absolute value than any positive real number. The surreals share many properties with the reals, including the usual arithmetic operations (addition, subtraction, multiplication, and division); as such, they form an ordered field . [a] If formulated in Von Neumann–Bernays–Gödel set theory , the surreal numbers are the largest possible ordered field; all other ordered fields, such as the rationals, the reals, the rational functions , the Levi-Civita field , the superreal numbers , and the hyperreal numbers , can be realized as subfields of the surreals. [1] It has also been shown (in Von Neumann–Bernays–Gödel set theory ) that the maximal class hyperreal field is isomorphic to the maximal class surreal field; in theories without the axiom of global choice , this need not be the case, and in such the...
Read more